php+mysql根据给定的经纬度查询数据库中与它最近的点

一个给定的数据库，存储的是一些已知地点以及他们的经纬度，内有43W多条的数据。
现在需要拿用户的经纬度和已知地点进行距离匹配，如果它们之间的距离小于一定的数据，比如说500米，就认为用户是在这个地点。
MYSQL本身是支持空间索引的，但是在5.x的版本中，取消了对Distance()和Related()的支持，参考这里：MySQL 5.1参考手册 :: 19. 中的空间扩展 19.5.6. 测试几何类之间空间关系的函数，无法使用空间的距离函数去直接去查询距离在一定范围内的点。所以，我首先想到的是，对每条记录，去进行遍历，跟数据库中的每一个点进行距离计算，当距离小于500米时，认为匹配。这样做确实能够得到结果，但是效率极其低下，因为每条记录都要去循环匹配40W条数据，其消耗的时间可想而知。经过记录，发现每条记录处理的时间消耗达到1700ms，针对每天上亿的数据量，这样一个处理速度，让人情何以堪啊。。。
我自己也有个想法，就是找到每条记录所在点的经纬度周围的一个大概范围，比方说正方形的四个点，然后使用mysql的空间计算，使用MBR去得出点在这个矩形内的已知记录，然后进行匹配。可惜，自己没想出能计算到四个点经纬度的方法。
意外的，查询到了一个关于这个计算附近地点搜索初探，里面使用python实现了这个想法。
所以参考了一下原文中的算法，使用PHP进行了实现。

实现原理也是很相似的，先算出该点周围的矩形的四个点，然后使用经纬度去直接匹配数据库中的记录。

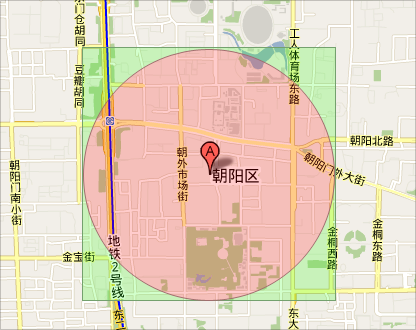
红色部分为要求的搜索范围，绿色部分我们能间接得到的结果范围

参考wiki百科上的一些球面计算公式：

假设已知点的经纬度分别为$lng, $lat
先实现经度范围的查询，
在haversin公式中令φ1 = φ2，可得:

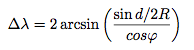
用PHP进行计算，就是：

//$lat 已知点的纬度
$dlng =  2 * asin(sin($distance / (2 * EARTH_RADIUS)) / cos(deg2rad($lat)));
$dlng = rad2deg($dlng);//转换弧度

然后是纬度范围的查询，
在haversin公式中令 Δλ = 0，可得

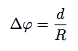
在PHP中进行计算，就是：

$dlat = $distance/EARTH_RADIUS;//EARTH_RADIUS地球半径
$dlat = rad2deg($dlat);//转换弧度

最后，就可以得出四个点的坐标：
left-top : (lat + dlat, lng – dlng)
right-top : (lat + dlat, lng + dlng)
left-bottom : (lat – dlat, lng – dlng)
right-bottom: (lat – dlat, lng + dlng)

我把以上方法写成了一个函数，综合起来就是：

/**
 *计算某个经纬度的周围某段距离的正方形的四个点
 *
 *@param lng float 经度
 *@param lat float 纬度
 *@param distance float 该点所在圆的半径，该圆与此正方形内切，默认值为10千米
 *@return array 正方形的四个点的经纬度坐标
 */
function returnSquarePoint($lng, $lat,$distance = 10)
{
    $radius = 6371; //地球半径，平均半径为6371km

    $dlng =  2 * asin(sin($distance / (2 * $radius)) / cos(deg2rad($lat)));
    $dlng = rad2deg($dlng);

    $dlat = $distance/$radius;
    $dlat = rad2deg($dlat);

    return array(
        'left-top'=>array('lat'=>$lat + $dlat,'lng'=>$lng-$dlng),
        'right-top'=>array('lat'=>$lat + $dlat, 'lng'=>$lng + $dlng),
        'left-bottom'=>array('lat'=>$lat - $dlat, 'lng'=>$lng - $dlng),
        'right-bottom'=>array('lat'=>$lat - $dlat, 'lng'=>$lng + $dlng)
    );
}

$squares = returnSquarePoint($lng, $lat);
$sql = select *,((ACOS(SIN($lat * PI() / 180) * SIN(`lat_baidu` * PI() / 180) + COS($lat * PI() / 180) * COS(`lat_baidu` * PI() / 180) * COS(($lng-`lng_baidu`) * PI() / 180)) * 180 / PI()) * 111.18957696) AS distance from `sales_service_point` where lat_baidu<>0 and lat_baidu>{$squares['right-bottom']['lat']} and lat_baidu<{$squares['left-top']['lat']} and lng_baidu>{$squares['left-top']['lng']} and lng_baidu<{$squares['right-bottom']['lng']} and status = 1 order by distance asc limit 10

左邻右舍